2118: Street Race

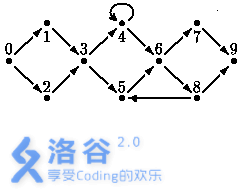
## 题目描述 图一表示一次街道赛跑的跑道。可以看出有一些路口（用 0 到 N 的整数标号），和连接这些路口的箭头。路口 0 是跑道的起点，路口 N 是跑道的终点。箭头表示单行道。运动员们可以顺着街道从一个路口移动到另一个路口（只能按照箭头所指的方向）。当运动员处于路口位置时，他可以选择任意一条由这个路口引出的街道。  图一：有 10 个路口的街道 一个良好的跑道具有如下几个特点： 每一个路口都可以由起点到达。 从任意一个路口都可以到达终点。 终点不通往任何路口。 运动员不必经过所有的路口来完成比赛。有些路口却是选择任意一条路线都必须到达的（称为“不可避免”的）。在上面的例子中，这些路口是 0，3，6，9。对于给出的良好的跑道，你的程序要确定“不可避免”的路口的集合，不包括起点和终点。 假设比赛要分两天进行。为了达到这个目的，原来的跑道必须分为两个跑道，每天使用一个跑道。第一天，起点为路口 0，终点为一个“中间路口”；第二天，起点是那个中间路口，而终点为路口 N。对于给出的良好的跑道，你的程序要确定“中间路口”的集合。如果良好的跑道 C 可以被路口 S 分成两部分，这两部分都是良好的，并且 S 不同于起点也不同于终点，同时被分割的两个部分满足下列条件：（1）它们之间没有共同的街道（2）S 为它们唯一的公共点，并且 S 作为其中一个的终点和另外一个的起点。那么我们称 S 为“中间路口 ”。在例子中只有路口 3 是中间路口。 ## 输入格式： 输入文件包括一个良好的跑道，最多有 50 个路口，100 条单行道。 一共有 N+2 行，前面 N+1 行中第 i 行表示以编号为(i-1)的路口作为起点的街道，每个数字表示一个终点。行末用 -2 作为结束。最后一行只有一个数字 -1。 ## 输出格式： 第一行包括：跑道中“不可避免的”路口的数量，接着是这些路口的序号，序号按照升序排列。 第二行包括：跑道中“中间路口”的数量，接着是这些路口的序号，序号按照升序排列。 ## 输入样例#1： ``` 1 2 -2 3 -2 3 -2 5 4 -2 6 4 -2 6 -2 7 8 -2 9 -2 5 9 -2 -2 -1 ``` ## 输出样例#1： ``` 2 3 6 1 3 ```